编者按:国外对套期保值的认识大致可以分为:消除与价格波动有关的风险、降低与价格波动有关的风险并从基差变动中获利、管理价格风险共三个过程;与之对应的,套期保值理论发展也主要经历三个阶段——传统套期保值理论、基差逐利型套期保值理论和现代套期保值理论。本文简单回溯了国外套期保值理论的历史演变,重点介绍第三阶段现代套期保值理论的数学基础、形成与发展过程。
一、套期保值的初级演变:从朴素的风险规避到主动追求基差套利
1.传统套期保值理论:完美套期保值与基差风险问题
最早的套期保值理论认为期货套期保值的目的是回避现货市场价格风险,把价格波动所造成的损失转嫁于投机者,因而将该行为视为一种“保险”。作为该理论派的代表人物之一,英国经济学家约翰·希克斯(John Hicks)在 1939 年出版的《价值与资本》中系统阐述了套期保值的基本逻辑。
按照该理论,一个持有实物商品(现货头寸)的生产商或贸易商为了“锁定”未来售价并消除价格波动的风险,会在期货市场上卖出等量(但方向相反)的合约。这种操作的隐含假设是套期保值比率(hedge ratio)应为1,即100%对冲现货头寸。如果现货头寸的亏损能被期货头寸的盈利完全抵消,那么这个套期保值就被认为是“完美的”。
然而,这一传统观点的核心缺陷在于它未能充分解释“基差风险”(Basis Risk),(基差=现货价格-期货价格)。传统理论的美好设想依赖于现货与期货价格的完美同步变动(即基差为零),但现实中两者几乎从不如此,因此期货市场的获利不一定能完全弥补现货市场的亏损:
基差会因为存储成本、市场预期、供需变化等因素而发生不可预测的变动,这意味着一个套期保值比率为1的对冲操作,其风险远未被完全消除,最终仍可能产生显著的盈利或亏损。
许多早期理论家将这个至关重要的问题降级到脚注中处理,未能给予其应有的重视。
2.沃金的贡献:为预期利润而套期保值
霍尔布鲁克·沃金(Holbrook Working)的研究从根本上挑战了传统观点。他观察到成熟的套期保值者并不仅仅是被动的风险规避者,而是积极的、以追求利润为目的的市场参与者。
在 1953 年发表的《期货交易与套期保值》中,沃金首次提出套期保值的核心是捕捉现货与期货价格差(基差)的变化机会,而非单纯对冲风险。他认为套期保值的决策核心在于对“基差”未来变化的预期。套期保值者关注的是相对价格(基差)的变动而非绝对价格水平的涨跌。
例如,一个持有现货的卖方套期保值者,如果预期基差将走弱(即现货价格相对于期货价格下跌),他就会进行套期保值——因为基差的有利变动将带来额外利润。反之,如果预期基差将走强,他可能会选择不进行套期保值。因此,在沃金看来,套期保值更像是一种基于现货与期货相对价格的套利行为。
沃金的理论将“预期”和“利润动机”这两个关键要素引入了套期保值理论,这是一个巨大的进步——他将分析的焦点从消除绝对价格风险转移到管理相对价格风险(基差风险)上。
然而,他的理论在很大程度上是定性的,未能提供一个形式化的框架来决定到底应该对冲“多少”头寸。沃金的理论虽然更贴近现实,但其内部存在一种无法自行解决的理论张力。通过引入利润动机,他实际上已将套期保值定义为一种投资决策。这就自然引出了一个核心问题:套期保值者应如何平衡基差有利变动带来的潜在利润与自身预期错误所带来的风险?
而马柯维茨的投资组合理论的闪亮登场,恰恰补齐了沃金的理论所缺乏的实操工具短板。可以说,沃金准确地识别出了决策中的两个关键变量——源于基差的预期回报和风险,但马柯维茨提供了用均值-方差优化来寻找两者最佳平衡点的数学工具。沃金的研究可以被视为一个关键的中间步骤,它将套期保值从纯粹的“保险”模型推向了“选择性承担风险”的模型,为最终的投资组合优化方法的登场做好了完美的铺垫。
二、马柯维茨革命:现代投资组合理论的基础
20世纪50年代,马柯维茨提供的核心理论工具箱对套期保值理论发展产生了重大影响,并被用于彻底革新套期保值理论。
1.均值-方差范式:风险与回报的量化
在马柯维茨之前,投资风险是一个模糊且主观的概念。他在1952年发表的论文中最革命性的贡献在于为投资风险提供了一个形式化、可量化的定义:资产回报的方差(variance)或标准差(standard deviation)。这一创举使得明确地对预期回报(“均值”)与风险(“方差”)之间的权衡关系进行建模成为可能。
该理论建立在一个核心假设之上:投资者是厌恶风险的(risk-averse)。这意味着对于给定的预期回报水平,投资者总是会选择风险最低的投资组合。反之,只有在获得更高预期回报的前提下,投资者才愿意承担更大的风险。这个看似简单的行为假设构成了整个优化框架的基石。
风险的量化是实现金融理论科学化的关键第一步。通过赋予风险一个明确的数学身份,马柯维茨使得系统性地管理风险成为可能,这就打破了以往依赖直觉和经验法则的局限。这一转变的意义远不止于提供计算公式,它为构建了一个全新的分析维度提供了基础。
传统的金融决策往往是单维度的,例如“最大化收益”或“最小化风险”。马柯维茨通过引入均值-方差框架,将投资决策置于一个二维空间中,任何投资组合都可以在这个由风险和回报定义的坐标系中被定位。
这一概念上的飞跃是后续理论发展的必要前提,它为将套期保值问题从单一的风险抵消操作重塑为一个双目标的优化问题铺平了道路。
2.分散化的力量:协方差与相关性的核心作用
马柯维茨用数学语言严谨地证明了分散化投资的价值,即人们常说的“不要把所有鸡蛋放在一个篮子里”。他指出,一个投资组合的总体风险并非组合内各资产风险的简单加权平均。相反,它同时取决于各资产自身的方差以及它们之间的协方差(covariance)或相关性(correlation)。
这是一个里程碑式的见解,因为在马柯维茨之前,分析师倾向于孤立地评估单一资产的风险而忽略了资产间的相互作用。对协方差的强调可以说是马柯维茨最深刻的贡献,它将投资的焦点从挑选单个的“明星资产”转移到构建一个高效的“投资组合”上。
在这个组合中,资产之间的互动关系变得至关重要。正是这一核心机制为理解套期保值的本质提供了关键的数学工具。套期保值的核心在于利用期货合约(一种资产)与现货头寸(另一种资产)之间的价格互动关系(即协方差)来降低整体头寸的风险。没有对协方差的深刻理解,现代套期保值理论的数学基础将无从谈起。
3.有效前沿与最优投资组合选择
基于均值-方差和分散化的原则,马柯维茨提出了有效前沿(Efficient Frontier)的概念。有效前沿是在风险-回报坐标图上由一系列“最优投资组合”(Efficient Portfolio)构成的集合。这些组合的“最优”体现在:对于任意给定的风险水平,它们能够提供最高水平的预期回报;或者对于任意给定的预期回报水平,它们的风险是最低的。
在图形上,有效前沿是一条向右上方凸出的曲线。位于曲线下方的任何投资组合都是次优的,因为在相同风险下存在回报更高的组合,或在相同回报下存在风险更低的组合。这条曲线的最左侧端点代表着所有可能组合中风险最低的一个,被称为最小方差组合(Minimum Variance Portfolio, MVP)。
当引入无风险资产(如短期国债)后,投资的可能性集合得到了极大的扩展。此时,有效前沿不再是一条曲线而是一条从无风险利率点出发与原有效前沿相切的直线,这条直线被称为资本市场线(Capital Market Line, CML)。这条切线上的所有投资组合都优于原有效前沿上的组合。
理论上,所有理性投资者都将持有一个相同的风险资产组合,即位于切点的“市场投资组合”(Market Portfolio),该组合拥有最高的夏普比率。投资者再根据自身的风险偏好决定在无风险资产和市场投资组合之间分配资金的比例。
有效前沿为最优投资决策提供了一个完整的理论框架。它为投资者绘制了一幅清晰的地图:展示了所有可能的最佳风险-回报组合,使他们能够根据自己的风险承受能力在有效前沿上选择一个最适合自己的投资组合。这个框架不仅改变了资产管理,也为其他金融决策的优化提供了强大的分析工具。
三、现代套期保值理论的逐步形成
1.概念性的突破(60年代初):约翰逊)与斯坦建立最初的桥梁
在马柯维茨的理论提出后不久,一些富有远见的学者便开始探索其在套期保值领域的应用。现代套期保值方法的真正起点源于约翰逊和斯坦等学者提出的一个概念性突破:被对冲的头寸不应再被看作是一个由期货合约提供“保险”的现货资产。相反,它应该被视为一个由两种资产构成的“投资组合”。这两种资产分别是:现货头寸(例如,一批铜的库存)、一个期货市场上的空头(或多头)头寸。
此时,套期保值者面临的问题不再是“如何消除风险?”,而是“如何构建一个由一个现货资产和一个期货资产组成的最优投资组合?”。决策的核心变成了为这个组合中的期货资产选择一个最优的权重,而这个权重,正是我们所说的套期保值比率。
利兰·L·约翰逊(Leland L. Johnson)是首批明确将套期保值者的决策建模为在“预期回报”和“风险”之间进行选择的学者之一。在其1960年的论文《商品期货中的套期保值与投机理论》中直接引用了投资组合选择的语言。他指出,套期保值者会同时持有被对冲和未被对冲的头寸,这并非一个“全有或全无”的决策而是一个旨在达到理想风险-回报状态的投资组合决策。
杰罗姆·L·斯坦(Jerome L. Stein)在其1961年的论文《现货与期货价格的同时决定》中,则构建了一个更为形式化的模型。在该模型中,一个库存持有者会根据已对冲库存和未对冲库存各自的预期回报与风险,来决定两者之间的分配比例。他明确使用了均值-方差框架,并在一个风险-回报坐标图上描绘了机会轨迹(opportunity locus)。
约翰逊和斯坦的开创性工作,共同为将套期保值视为一个投资组合问题奠定了坚实的理论基础,他们是连接套期保值理论与MPT的第一座桥梁。
2.埃德林顿(1979):将套期保值有效性实证化为方差的降低
如果说约翰逊和斯坦完成了理论构建,那么路易斯·H·埃德林顿(Louis H. Ederington)则通过其1979年的论文《新兴期货市场的套期保值表现》提供了关键的实证应用和一个简洁而强大的衡量标准。他认为:
套期保值的目标是风险最小化,通过建立期货头寸对冲现货价格波动风险,使组合收益的方差最小化。
有效性衡量需量化比较,提出用方差减小率(Variance Reduction Rate, VRR)作为套期保值效果的评估标准,即套期保值后组合收益方差相对于未套期保值现货收益方差的下降比例。
基差风险替代价格风险,套期保值并非完全消除风险,而是将现货价格波动风险转化为基差波动风险(即现货价与期货价之差)
埃德林顿将套期保值的有效性(effectiveness, 记为e)定义为:通过最优套期保值所实现的方差降低相对于未对冲头寸方差的百分比。其公式为:

马柯维茨的理论于1952年诞生,在十年之内约翰逊和斯坦便发表了将其应用于套期保值的理论模型,这相当于“理论假说”阶段。然而,在之后近二十年的时间里,这一思想在很大程度上仍停留在学术层面。
埃德林顿1979年的论文则标志着“实验验证”阶段的到来。他将套期保值的投资组合理论转化为一个简单、稳健且可操作的度量标准,并将其应用于真实的市场数据。
四、套期保值理论仍在持续发展与完善
1.对均值-方差框架在套期保值应用中的批判性评估
尽管基于MPT的套期保值模型具有革命性意义,但它建立在一系列理想化的假设之上,这些假设在现实世界中面临挑战。
理性人假设的局限:MPT假设投资者是完全理性的、追求期望效用最大化的个体。然而,行为金融学的研究表明,现实中的决策者会受到各种认知偏差的影响,例如“熟悉度偏见”(familiarity bias),即投资者倾向于投资自己熟悉的领域,这可能导致投资组合过于集中,无法有效分散风险。
对历史数据的依赖:模型的关键输入参数——方差、协方差和相关性——通常是基于历史数据估算的。然而,这些参数在时间上是极不稳定的,尤其是在市场危机期间,资产间的相关性可能发生剧烈且出人意料的变化。这给依赖该模型进行套期保值的实践者带来了巨大的挑战。
风险度量的片面性:将标准差作为风险的唯一度量是一个显著的局限。标准差同等地对待了上行波动(潜在收益)和下行波动(潜在损失),这与大多数投资者,特别是企业套期保值者对风险的直观感受不符。套期保值者的主要目标是防范重大损失,而非限制超额收益。
计算复杂性:对于包含大量资产的投资组合,计算完整的协方差矩阵在计算上变得非常复杂和耗时,这在一定程度上限制了原始模型在大型机构中的直接应用。
2.现代理论的持续发展与延伸
MPT框架的局限性并未使其遭到摒弃,反而激发了大量的后续创新,这些创新共同定义了并丰富了现代量化风险管理。
替代性风险度量:认识到方差的不足,现代风险管理发展并采纳了其他风险度量指标。例如,风险价值(VaR)专注于在给定置信水平下可能发生的最大损失,这更符合套期保值者的核心关切。最优套期保值比率可以被重新推导,以最小化VaR而非方差。其他模型则采用下行风险度量,如索提诺比率(Sortino Ratio)。
动态套期保值:马柯维茨模型本质上是静态的,它假设一个单期的投资视界。但在现实中,套期保值是一个持续的动态过程。现代方法采用时间序列模型,如GARCH模型族,来捕捉随时间变化的波动率和相关性,从而计算出能够根据市场状况动态调整的套期保值比率。
融合行为因素:越来越多的研究试图将投资者情绪和其他心理因素量化,并将其纳入投资模型,以期改进经典MPT的纯理性假设,提高模型的现实解释力。
综上所述,哈里·马柯维茨的投资组合理论为现代套期保值理论提供了概念和数学上的双重基石,利兰·约翰逊,杰罗姆·斯坦的开创性工作,共同为将套期保值视为一个投资组合问题奠定了坚实的理论基础,路易斯·埃德林顿则进一步将套期保值的投资组合理论转化为一个简单、稳健且可操作的度量标准,并将其应用于真实的实践,共同将套期保值理论推向第三个阶段。
可以说,现代投资组合理论是现代风险管理这棵大树的根基和主干,它将套期保值从一门基于经验和直觉的艺术转变为一门基于严谨数学和统计分析的科学。所有新的分支——动态套期保值、复杂的风险度量、行为量化模型——都源于对解决原始主干所固有挑战的追求。
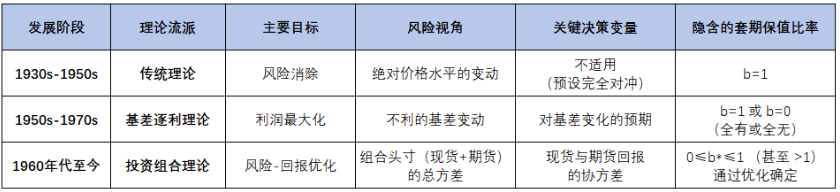
表:国外套期保值理论发展的三个阶段